March 14th is \(\pi\)-day in the US (and perhaps \(4.\overline{666}\) day in Europe). The idea of a day devoted to celebrating an important irrational number is wonderful — I’d love to see schools celebrate e-day as well, but February 71st isn’t on the calendar. Unfortunately, March 14th has also become the day in which 4th and 5th graders around the US practice for one of the most pointless exercises imaginable – a competition to recite the largest number of digits of \(\pi\).
March 14th is \(\pi\)-day in the US (and perhaps \(4.\overline{666}\) day in Europe). The idea of a day devoted to celebrating an important irrational number is wonderful — I’d love to see schools celebrate e-day as well, but February 71st isn’t on the calendar. Unfortunately, March 14th has also become the day in which 4th and 5th graders around the US practice for one of the most pointless exercises imaginable – a competition to recite the largest number of digits of \(\pi\).
Memorization of long digit strings is not an exercise that teaches a love of mathematics (or anything else useful about the natural world). This is solely an exercise in recall, which is perhaps valuable for remembering phone numbers, but not for understanding transcendental constants. For all practical purposes, only the first few digits of \(\pi\) are really necessary – the first 40 digits of \(\pi\) is enough to compute the circumference of the Milky Way galaxy with an error less than the size of an atomic nucleus.
So, because \(\pi\) is a such an accessible entry to mathematics and science, I thought I’d come up with a list of other cool \(\pi\) things that could replace these pointless memory contests:
- The earliest written approximations of \(\pi\) are found in Egypt and Babylon, and both are within 1 percent of the true value. In Babylon, a clay tablet dated 1900–1600 BC has a geometrical statement that, by implication, treats \(\pi\) as 25/8 = 3.1250. In Egypt, the Rhind Papyrus, dated around 1650 BC, but copied from a document dated to 1850 BC has a formula for the area of a circle that treats \(\pi = \left(\frac{16}{9}\right)^2 \approx 3.1605\).
- In 220 BC, Archimedes proved that \( \frac{223}{71} < \pi < \frac{22}{7}\). The mid-point of these fractions is 3.1418.
- Around 500 AD, the Chinese mathematician Zu Chongzhi was using a rational approximation for \(\pi \approx 355/113 = 3.14159292\), which is astonishingly accurate. For most day-to-day uses of \(\pi\) this particular approximation is still sufficient.
- By 800 AD, the great Persian mathematician, Al-Khwarizmi, was estimating \(\pi \approx 3.1416\)
- A good mnemonic for the decimal expansion of \(\pi\) is given by the letter count in the words of the sentences: “How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics. All of thy geometry, Herr Planck, is fairly hard…”
- Georges-Louis Leclerc, The Comte de Buffon came up with one of the first “Monte Carlo” methods for computing the value of \(\pi\) in 1777. This method involves dropping a short needle of length \(\ell\) onto lined paper where the lines are spaced a distance \(d\) apart. The probability that the needle crosses one of the lines is given by: \(P = \frac{2 \ell}{\pi d}\).
- In 1901, the Italian mathematician Mario Lazzarini attempted to compute \(\pi\) using Buffon’s Needle. Lazzarini spun around and dropped a 2.5 cm needle 3,408 times on a grid of lines spaced 3 cm apart. He got 1,808 crossings and estimated \(\pi = 3.14159292\). This is a remarkably accurate result! There is now a fair bit of skepticism about Lazzarini’s result, because his estimate reduces to Zu Chongzhi’s rational approximation. This controversy is covered in great detail in Mathematics Magazine 67, 83 (1994).
- Another way to estimate \(\pi\) would be to use continued fractions. Although there are simple continued fractions for \(\pi\), none of them show any obvious patters. There’s a beautiful (but non-simple) continued fraction for \(\frac{4}{\pi}\):
\(\frac{4}{\pi} = 1 + \frac{1^2}{2 + \frac{3^2}{2 + \frac{5^2}{2 + \frac{7^2}{2 + …}}}}\)Can you spot the pattern?
- Vi Hart, the wonderful mathemusician, has a persuasive argument that we should instead be celebrating \(\tau\) day on June 28th. Actually, all of her videos are wonderful. If my kids spent all day doing nothing but playing with snakes it would be better than memorizing digits of \(\pi\).
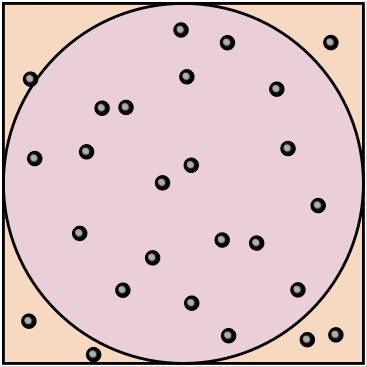
- Another wonderful way to compute \(\pi\) is to use nested round and square baking dishes (of the correct size) and drop marbles into them randomly from a distance. Simply count up the number of marbles that land in the circular dish and keep track of the total number of marbles that landed in either the circle or the square. Since the area formulae for squares and circles are related, the value of \(\pi = 4 \frac{N_{circle}}{N_{total}}\).
There are probably 7000 better things to do with \(\pi\) day than digit memory contests. There are lots of creative teachers out there — how are all of you going to celebrate \(\pi\)-day?